|可以人为的调制引力波吗?|
图1 两颗中子星相互产生的引力波的二维表示。

百科:在爱因斯坦的广义相对论中,引力被认为是时空波折的一种效应。这种波折是由于质量的存在而导致。常日而言,在一个给定的体积内,包含的质量越大,那么在这个体积边界处所导致的时空曲率越大。当一个有质量的物体在时空当中运动的时候,曲率变革反应了这些物体的位置变革。在某些特定环境之下,加速物体能够对这个曲率产生变革,并且能够以波的形式向外以光速传播。这种传播征象被称之为引力波。
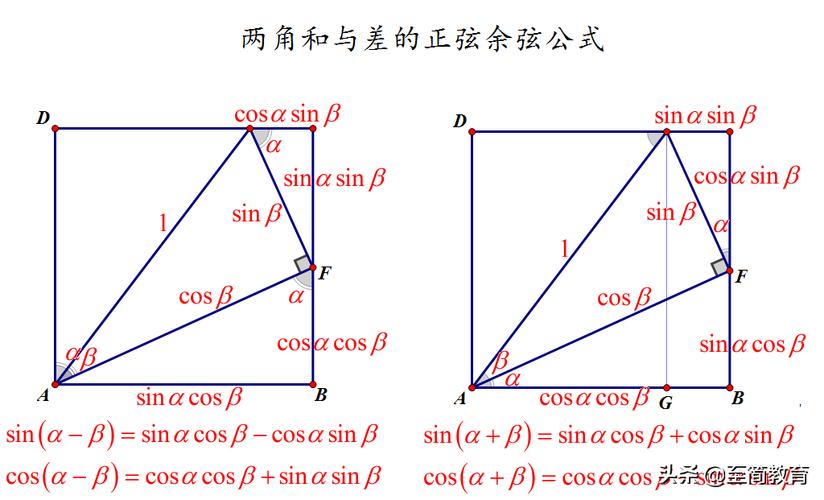
图2 引力波探测数据
LIGO丈量的引力波在汉福德(左)和利文斯顿(右)探测器,与理论预测值比较。
|言归正传|
下图3是一个Signal旗子暗记,它的AM(Amplitude Modulation)幅度调制旗子暗记与FM(Frequency Modulation)频率调制旗子暗记。这是韶光域上我们所瞥见的,我们随意马虎看出的是AM旗子暗记的振动幅度变革明显,FM旗子暗记的频率随着韶光“又紧又松”。
图3 AM与FM调制旗子暗记
在高中学习三角函数之时,一定学习积化和差公式,当时为了这个背这些公式,真是什么手段都用上了。(哥-哥=负嫂嫂,这个梗能看懂的点个赞!
)
你不会想到这个公式,竟然成为我们通信技能中的根本公式。
调制,在韶光域上便是一个乘法操作,在频域上就相称于频谱的搬移。基带旗子暗记为m(t),
粗暴一点,载波旗子暗记有多种,我们这里说调制便是乘上一个角频率为Wc=2πfc的余弦旗子暗记,
得到要发射的射频旗子暗记,也叫做已调旗子暗记,
这里面用到了三角函数的积化和差公式,看到没,调制后的旗子暗记里面包含了两个频率身分Wc-W和Wc+W。此时,m(t)是一个低频率的旗子暗记,例如10kHz,而载波c(t)是一个高频率旗子暗记,例如10MHz,那么调制后旗子暗记频率分为9.99MHz和10.01MHz,都在10MHz附近。也便是说,调制技能把旗子暗记搬运到了载波频率附近。
再来看一下频域中的情形,我们知道余弦函数的傅里叶变换是对应频率处的冲激,那么利用傅里叶变换的频移性子,我们可以得出旗子暗记的频谱。
图4 AM旗子暗记的调制过程
文章链接:仿照调制:我们为什么要调制?先从AM幅度调制开始
经由调制之后,已调旗子暗记的频谱已平移至载波频率的两边了,此时得到已调旗子暗记的带宽Bam是基带旗子暗记的两倍,Bam=2Wh。
相关解调通信中,发射机通过某一信道传输旗子暗记,吸收机卖力吸收。信道是一种物理介质。旗子暗记在经由信道的过程时,一定会产生变革。俗话说“雁过留声”不便是这个道理吗?
图5 通信过程
一样平常来说,信道会改变经由它的旗子暗记。
如果假定信道不改变旗子暗记,于是吸收到的旗子暗记便是我们刚才调制过的旗子暗记。吸收到这种旗子暗记后,我们须要从中规复出基带旗子暗记。吸收到的旗子暗记假设为coswtcoswct,那么我们再次用一个载波旗子暗记乘以吸收到的旗子暗记,得到
解调后的旗子暗记包括了一个低频旗子暗记m(t)和一个高频身分m(t)cos2wct。此时,用一个装置,这个装置只能通过低频率无法通过高频率,号称“低通滤波器\"大众,可以把高频身分过滤掉,这样就得到要通报的基带旗子暗记了。
实在对付吸收到的旗子暗记,如果作傅里叶变换,可以得到其频谱表达式为,
频谱表达式可以看出低频部分为M(w),高频部分为w-2wc和w+2wc,将高频身分滤掉,就得到了基带旗子暗记。
这个解调过程叫作相关解调。
全体过程可以用框图这样表示。
图6 相关解调过程
相关解调的难点在于要在吸收机侧产生一个与发射机侧同频同相的载波旗子暗记。便是图6中确当地振荡器。
硬件实现上面谈了一些理论,详细用电路怎么搭建?
乘法器如何实现呢,可以用差分放大器实现。
不过,现在基本上都有现成的芯片可以用。以是如果想理解个中事理,可以自行学习“仿照电子线路”,班长后期也会写到这块!
图7 乘法器实现电路
重点说说低通滤波器。
这个\"大众低通\公众便是低频率随意马虎通过,高频率难以通过;滤波是将旗子暗记中特定频率段滤除的操作,是抑制和防止滋扰的一项主要方法。
这里面就用了RC电路了,这个班长之前与大家聊过,当时文章写得较为粗糙:
「百科」1分钟理解RC、RL、RLC电路事理
图8 RC低通滤波器
上图是一个范例的低通滤波器,互换电路中电容器的电容电抗如下:
如果把电容C换成电阻R2,那么很随意马虎通过欧姆定律得出Vout;再把电容请回来,互换电路中阻碍电流流动的称为阻抗,符号Z;对付由单个电阻与单个电容串联组成的串联电路,电路输出电压可以按如下打算:
如果我们用不同频率的余弦互换旗子暗记,输入这个别系,那么输出Vou也会随着频率不断变革。
以频率为横坐标,Vout/Vin为纵坐标,画出的函数图形叫做频率相应图,也叫做波特图。
BODE图9显示了滤波器的低频频率相应险些是平坦的,所有输入旗子暗记都直接通报到输出端,从而得到了近1倍的增益,直到达到其截止频率点(ƒc)。这是由于电容器的阻抗在低频时很高,并且阻挡了任何电流利过电容器。
图9 低通频率相应
对付这个截止频率点ƒc以上的任何高频旗子暗记,经由低通滤波电路都会大大衰减,即它们会迅速减小。这是由于在非常高的频率下,电容器的阻抗变得如此之低,甚至于输出端靠近短路。
然后,通过仔细选择精确的电阻-电容组合,我们可以创建一个RC电路,它许可一定值以下的频率范围不受影响地通过电路,而运用于这个截止频率点以上的任何频率都会被衰减,从而产生一个常日被称为低通滤波器的电路。
对付这种\公众低通滤波器\"大众电路,凡是低于ƒc点的旗子暗记,很少或险些没有衰减,并被认为是在滤波器通带区。此通带区域还表示滤波器的带宽。在此点以上的任何旗子暗记常日被认为是在滤波器停滞带区,它们将被大大衰减。
总结本篇从调制提及,聊了相关解调,大略先容了RC低通滤波器电路,总体内容没有详细展开,试图给读者观点上的认识。
调制,解调,滤波器每一个领域都可以写一本书,班长会定期更新,希望大家支持!
@通信M班长
Reference:通信之道(杨学志),通信事理(樊昌信),部分图片内容来源于网络,感谢!















